Formulario: trigonometria. Risoluzione dei triangoli
Risoluzione dei triangoli rettangoli
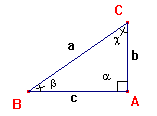
1° Teorema
In un triangolo rettangolo, la misura di un cateto è uguale al prodotto della misura dell’ipotenusa per il seno dell’angolo opposto oppure per il coseno dell’angolo adiacente.
`b = a sin beta` , `c = a sin gamma`
`b = a cos gamma` , `c = a cos beta`
2° Teorema
In un triangolo rettangolo, la misura di un cateto è uguale a quella dell’altro cateto per la tangente dell’angolo opposto al primo, o per la cotangente dell’angolo adiacente.
`c = b tan gamma` , `b = c tan beta`
`c = b cot beta` , `b = c cot gamma`
Area di un triangolo qualsiasi.
L’area di un triangolo qualsiasi è uguale al semiprodotto delle misure di due suoi lati per il seno dell’angolo fra essi compreso.
`text(Area) = (a b sin gamma)/2 = (b c sin alpha)/2 = (a c sin beta)/2`
Risoluzione dei triangoli qualsiasi.
Teorema dei seni (o di Eulero)
In un triangolo qualunque è costante il rapporto tra la misura di un lato e il seno dell’angolo opposto:
`a/(sin alpha) = b/(sin beta) = c/(sin gamma)`
Nota. Questi rapporti sono dunque costanti e la costante è la misura del diametro della circonferenza circoscritta, per cui è possibile enunciare il seguente:
Teorema della corda
In un triangolo il rapporto tra la misura di un lato e il seno dell’angolo opposto è uguale al diametro della circonferenza circoscritta:
`a/(sin alpha) = b/(sin beta) = c/(sin gamma) = 2r`
Vedi il terorema della corda
Teorema del coseno (o di Carnot)
In un triangolo qualsiasi il quadrato di un lato è uguale alla somma dei quadrati degli altri due diminuita del doppio prodotto di questi due lati per il coseno dell’angolo fra essi compreso:
`a^2 = b^2 + c^2 - 2bc cos alpha`
`b^2 = a^2 + c^2 - 2ac cos beta`
`c^2 = a^2 + b^2 - 2ab cos gamma`
Nota. Il teorema di Carnot generalizza il Teorema di Pitagora, a cui si riduce se si considera un triangolo rettangolo.
Teorema delle proiezioni
In un triangolo qualunque, la misura di un lato è uguale alla somma dei prodotti delle misure di ciascuno degli altri due per il coseno degli angoli che essi formano con il primo:
`a = b cos gamma + c cos beta`
`b = a cos gamma + c cos alpha`
`c = a cos beta + b cos alpha`
IN PRATICA
Per risolvere un triangolo qualsiasi devono essere noti tre elementi di cui almeno un lato. Dunque si possono presentare quattro casi:
-
due angoli e un lato (il problema presenta una sola soluzione)
- tre lati (il problema presenta una sola soluzione)
- due lati e l’angolo compreso (il problema presenta una sola soluzione)
- due lati e un angolo opposto ad uno di essi (il problema può avere nessuna, una o due soluzioni).
