Lunghezza della circonferenza: `C = 2 pi r`
Area del cerchio: `A = pi r^2`
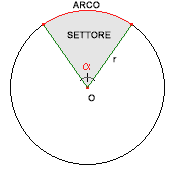
Lunghezza dell'arco: `l = (C * alpha)/(360)` con `alpha` misurato in gradi
Area del settore circolare: `A = (pi r^2 alpha)/360`; `A = 1/2 r^2 alpha`
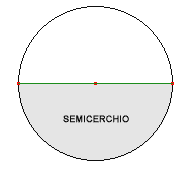
Area del semicerchio: `A = 1/2 pi r^2`
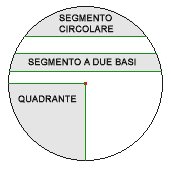
Area del quadrante: `A = 1/4 pi r^2`
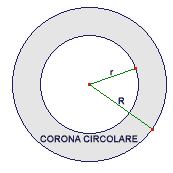
Area della corona circolare: `A = pi (R^2 - r^2)`
Area del segmento circolare: si trova come differenza fra l'area di un settore e l'area di un triangolo.
Raggio = `r`
In una circonferenza la misura di una corda è uguale al prodotto della misura del diametro per il seno di uno degli angoli alla circonferenza che insistono sulla corda.
`bar(AB) = 2r \ sin alpha`,
`bar(AB) = 2r \ sin (180 - alpha)`,
dove `alpha` è uno qualsiasi degli angoli alla circonferenza inscritti nell'arco maggiore `hat(AB)`.
Vedi anche il terorema dei seni
Se in una circonferenza due corde si intersecano, i segmenti che si formano sulla prima corda e quelli che si formano sulla seconda sono, rispettivamente, i medi e e gli estremi di una stessa proporzione.
`PA * PB = PC * PD`, ossia
`bar(PB) : bar(PD) = bar(PC) : bar(PA)`
Se da un punto esterno `P` a una circonferenza si conducone due secanti e si considerano i segmenti che hanno un estremo in `P` e l'altro in ciascuno dei punti di intersezione, i segmenti sulla prima secante sono gli estremi e i segmenti sulla seconda i medi di una stessa proporzione.
`PA * PB = PD * PC` , ossia `PA : PD = PC : PB`
Se da un punto `P` esterno a una circonferenza si tracciano una secante e una tangente, il segmento di tangente che ha per estremi `P` e il punto di contatto è medio proporzionale fra i segmenti di secante che hanno per estremo `P` e ciascuno dei punti di intersezione.
`PT^2 = PA * PB`, ossia `PA : PT = PT : PB`
Prova a muovere i punti `A` o `D` dei due segmenti o il punto `P` esterno alla circonferenza per vedere come varia la situazione geometrica descritta dal teorema delle secanti.
Se muovi un estremo del segmento lungo la circonferenza, per es. `D`, fino a farlo coincidere con l'altro, `C`, ottieni la situazione descritta nel teorema della tangente e della secante, dove `D = C = T`.