|
|||
FORMULARIO: funzioni iperboliche e loro inverse
|
|
||
|
Funzioni iperboliche |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
definizione geometrica:
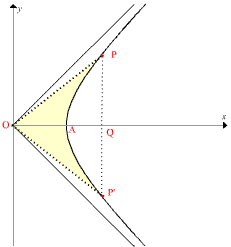
Data l’iperbole equilatera di equazione OA = a , OQ = x, PQ = y . Indicato con r il rapporto tra l’area del triangolo mistilineo OPAP’ ed il quadrato costruito su OA, per definizione si ha :
Nel caso in cui a = 1 le relazioni diventano:
|
definizione esponenziale: per conoscere i valori che le funzioni iperboliche assumono al variare di r, è utile esprimerle in forma esponenziale.
È ora possibile definire sei funzioni iperboliche del tipo y = f(x) , ove x ha lo stesso significato di r.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Relazioni fondamentali
In base a queste relazioni è possibile esprimere ogni funzione iperbolica in funzione delle altre:
Prendere il segno (+) o (–) a seconda che sia |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Relazioni di simmetria
|
Formule di duplicazione
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Funzioni iperboliche inverse |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Delle sei funzioni iperboliche si possono definire le corrispondenti funzioni inverse.
|
Definizione logaritmica
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
avente per asintoti le rette 
ed 
e semiasse reale -a. Su uno dei due rami consideriamo un punto P di coordinate x, y. Si ha quindi:
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
o 
.
; 
; 
; 
; 
.
con 
e 
con 
e 
con 
e 
con 
e 
con 
e 
con 
e 
per qualunque x
con 
con 
con 
con 
e 
|